أنماط التعلم - ما هي أنماط التعلم لدى المتعلمين

استخدام المقاييس الإحصائية في تحليل تفاوتات البيانات: دراسة الانحراف والتشتت

الإحصاء هو أساس لا غنى عنه في تحليل البيانات. حيث يتيح لنا فهم الاتجاهات والأنماط. ويساعد في اتخاذ القرارات المستندة إلى الأدلة. عندما نتحدث عن "البيانات الإحصائية". فإننا نشير إلى مجموعة واسعة من الأدوات والتقنيات التي تُمكننا من استخراج معلومات قيمة من كميات هائلة من البيانات.

في مجال الأعمال والتسويق. تُستخدم الأساليب الإحصائية لتقييم أداء المنتجات والخدمات. وفهم احتياجات العملاء، وتحديد فرص النمو. على مستوى الشركات، يمكن أن يكون الإحصاء أداة فعالة لفهم السوق. وتطوير استراتيجيات ناجحة، وتحسين رضا العملاء.

هذه المقدمة تهدف إلى توضيح دور الإحصاء في تحليل البيانات. وكيف يمكن توظيف هذه الأدوات لتحقيق أهداف مختلفة. سنستعرض في هذه المناقشة بعض الطرق التي يمكن من خلالها. استخدام الإحصاء لفهم البيانات واستخلاص المعلومات التي تدعم اتخاذ القرارات.

اقرأ أيضاً ماهو الفرق بين بيانات العينة وبين المتغير العشوائي؟ 

أوجد المتوسط الحسابي، الوسيط، مقدار التباين وقيمة الانحراف إذا كان لدينا القيم التالية

الحالة الأولى a : من رقمك الجامعي خذ كل رقم على حدا ثم اضف الى المجموعة رقمي 15 و 21

مثلا لو كان رقمك c1088211 اذا ستحسب المطلوب ل هذه الأرقام 1,0,8,8,2,1,1,15,21

الإجابة:

باعتبار رقمي الجامعي هو c1088211 وبالتالي سنطبق ما هو مطلوب مننا على الأرقام التالية:

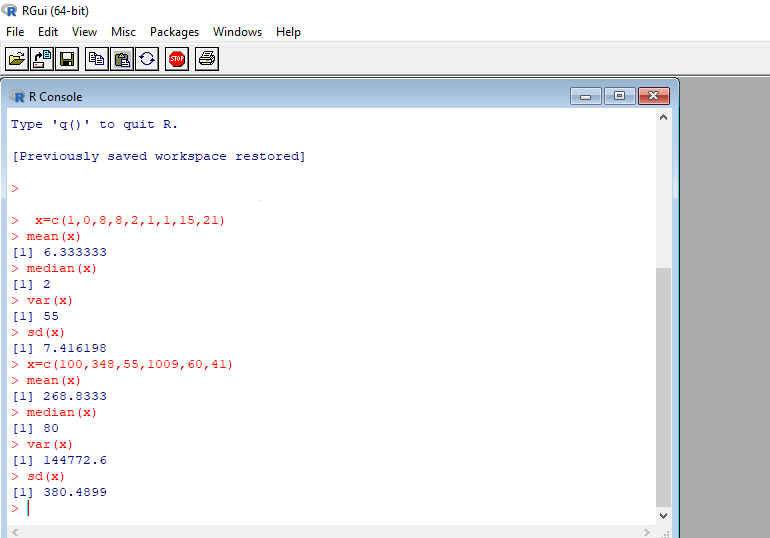
1,0,8,8,2,1,1,15,21 ويكون الناتج كما في المخطط التالي:

حيث المتوسط الحسابي (mean) = 6.333333.

الوسيط (median) = 2.

مقدار التباين (var) = 55.

قيمة الانحراف المعياري (sd) = 7.416198   .

الحالة الثانية b : 100, 348, 55, 1009 .

ضع أيضا رقمين عشوائين من اختيارك في الحالة الثانية من فئة العشرات مثلا 60 و 41.

بنفس الطريقة السابقة نطبق الأرقام الجديدة ونحسب المطلوب وتكون النتائج للحالتين السابقتين مبينة بالمخطط التالي:

تمرين حسابي.

أراد عمدة مدينة أن يعرف متوسط دخل الأفراد في هذه المدينة. يسكن المدينة 2,489,439 نسمه. ماهو المقياس المناسب لمعرفة متوسط الدخل للفرد هنا؟

متوسط دخل الفرد = الناتج الإجمالي / عدد السكان

باعتبار عدد السكان كبير جداً فلا يمكن حساب الناتج الإجمالي بسهولة. لذا نأخذ عينة من السكان. وتعتبر مقاييس النزعة المركزية أو ما يطلق عليه اسم المتوسطات. من اهم المقاييس التي يمكن البحث فيها للباحث الاحصائي. ومقباس النزعة المركزية يشير إلى القيمة التي عادة ضمن توزيعاً معيناً. 

ومتوسط أي ظاهرة يعبر عن المستوى العام لتلك الظاهرة. أو هو القيمة التي تتمركز حولها باقي القيم ولهذا السبب يطلق اسم المتوسطات على مقاييس النزعة المركزية (الحمزة، 2023، ص41).

لدينا عدد كبير من المقاييس التي درسناها في هذه الوحدة مثل المتوسط الحسابي والوسيط والمنوال وغيرها.

إذا أردت أن تعرف عدد أصدقائك الذين يشجعون نادي كرة القدم الذي تشجعه. فأي من المقاييس ستستخدم؟

إذا أردت أن أعرف عدد أصدقائي الذين يشجعون نادي كرة القدم الذي أشجعه. فسأحتاج إلى استخدام مقياس إحصائي من مقاييس النزعة المركزية. وذلك لأن هدفي معرفة عدد الأصدقاء. أي معرفة – مركز – مجموعة البيانات (وهو عدد المشجعين لنادي كرة القدم).

ومن ثم تبعاً لطبيعة البيانات نجد أن البيانات هنا هي – عدد المشجعين – لكل صديق، وهي بيانات – فئوية – (منفصلة، وليست متصلة).

لذا فالمقياس المناسب هو المنوال. وهو القيمة الأكثر شيوعًا في مجموعة البيانات. وأسهل مقاييس النزعة المركزية (محمد، د – ت، ص4).

في هذه الحالة، سيكون المنوال هو عدد المشجعين لنادي كرة القدم الذي يشجعه – أكبر عدد – من أصدقائي.

سنستخدم مقياس المنوال رغم أنه لا يعطي إجابة واضحة. ولكن يعبر عن القيمة المتكررة في موضوع مشجعي النادي هنا. ولا يتأثر بقيم متطرفة ومنه يمكن قياس البيانات النوعية. لذلك فالمنوال هو المقياس الممكن استخدامه في هذه الحالة.

ناقش صحة الادعاء التالي: 

المقاييس التي تحاول أن تصف نقطة تجمع المشاهدات هي مقاييس التشتت بينما المقاييس التي تحاول قياس مدى تبعثر البيانات عن متوسطها هي مقاييس النزعة المركزية. وضح إجابتك باستخدام أمثلة إذا لزم الأمر

هذا الادعاء غير صحيح، والتفسير يكون من خلال تعريف كل من النزعة المركزية ومقياس التشتت كالتالي:

النزعة المركزية هي تجميع عدد كبير من المفردات حول قيمة المتوسط. حيث يقل عدد المفردات تدريجياً بالابتعاد عن قيمة المتوسط. كما يوجد عدة مقاييس لقياس القيمة المتوسطة كالمتوسط الحسابي أو الوسيط

وبالتالي فمقاييس النزعة المركزية: هي مقاييس إحصائية تصف "مركز" مجموعة البيانات. تشمل مقاييس النزعة المركزية: الوسط الحسابي. وهو متوسط ​​جميع القيم في مجموعة البيانات. الوسيط وهو القيمة التي تقسم مجموعة البيانات إلى مجموعتين متساويتين. والمنوال هو القيمة الأكثر شيوعًا في مجموعة البيانات.

أما مقاييس التشتت فهي مقاييس إحصائية تصف "انتشار" مجموعة البيانات حول مركزها. تشمل مقياس التباين وهو متوسط ​​مربعات المسافات بين كل قيمة والوسط الحسابي. والانحراف المعياري هو الجذر التربيعي للتباين.

ومقياس التشتت هو الفرق بين قيمة المفردات أو البيانات أو المعلومات بين مجتمعين. ومعدل التشتت والتباعد بينهما هو معيار التشتت. وأهم مقاييسه المدى المطلق، والانحراف المتوسط والمعياري وغيره. ولكن بمقياس النزعة المركزية لدينا أنواع من القصور. لأنه قد تتساوى لدينا متوسط مجموعتين. ولكن يختلفان ببعض الصفات الأخرى. فلذلك نلاحظ ظهور مقياس التشتت.

أمثلة:

يكون الوسط الحسابي هو مقياس للنزعة المركزية. كما في المثال: إذا كانت لدينا مجموعة من درجات اختبار {80، 70، 90، 85، 75}، فإن الوسط الحسابي هو 80.

التباين هو مقياس للتشتت. كما في المثال: باستخدام نفس مجموعة درجات الاختبار، يكون التباين هو 25.

وبالتالي فمقاييس النزعة المركزية تصف "مركز" مجموعة البيانات. بينما مقاييس التشتت تصف "انتشار" مجموعة البيانات حول مركزها.

وبالتالي من خلال تعاريف التشتت والنزعة المركزية. نلاحظ عدم صحة الادعاء في المثال. وهي وصف نقطة التجمع للمشاهدات بمقياس التشتت. ومقياس مدى تبعثر البيانات بمقياس النزعة المركزية.

المراجع.

1. الحمزة، عبد الحليم. (2023). كتاب بيداغوجي في الإحصاء 1. كلية العلوم الاقتصادية والعلوم التجارية وعلوم التسيير. جامعة العربي التبسي. تبسة. الجزائر.
2. محمد، سندس عبد الكريم. (د - ت). مقاييس النزعة المركزية – إحصاء عام. المحاضرة الرابعة. جامعة البصرة. تم الاسترجاع من الرابط https://faculty.uobasrah.edu.iq/uploads/teaching/1651848606.pdf.