أنماط التعلم - ما هي أنماط التعلم لدى المتعلمين

كيف تحسب أرباح الأسهم؟ 

تُعد أسواق الأسهم من أهم الأدوات المالية التي تُتيح للأفراد والشركات فرصة الاستثمار وتحقيق الأرباح. ومن أجل اتخاذ قرارات استثمارية ناجحة. يعتمد المستثمرون على تحليل البيانات والنماذج الرياضية لفهم سلوك أسعار الأسهم والتنبؤ بحركتها المستقبلية. فتحليل سوق الأسهم مهم لاتخاذ قرارات استثمارية مدروسة (الاستثمار في التداول، 2024).

تمثل الدوال الرياضية. مثل f(t). التي تصف سعر السهم كدالة للزمن. وسيلة فعالة لدراسة الاتجاهات والتغيرات. باستخدام أدوات رياضية مثل الدوال الخطية. والمشتقات. والنسب المثلثية. يمكن تحليل بيانات الأسعار لتحديد أفضل الأوقات للشراء أو البيع.

من خلال هذا التحليل الرياضي المدعوم بالمنطق الكمي. يستطيع المستثمرون تقليل المخاطر وتعظيم العوائد. مما يُبرز الدور الحاسم للرياضيات في عالم الأسواق المالية.

إذا كنت تدرس دالة f(t) التي تمثل سعر السهم مع مرور الوقت. هناك العديد من الأدوات والمفاهيم التي قد تكون تعلمتها ويمكنك تطبيقها لتحقيق أرباح عن طريق شراء وبيع الأسهم. إليك بعضها:

الدالة الخطية التي يمثلها المستقيم

يمكنك استخدام التحليل الخطي لتقدير الاتجاه العام للسهم. إذا كان ميل الخط (المشتقة) إيجابيًا. فقد يشير ذلك إلى ارتفاع السعر. مما يجعله وقتًا جيدًا للشراء. وإذا كان الميل سلبيًا. 

فقد يشير ذلك إلى انخفاض السعر. وهو وقت مناسب للبيع. حيث تعتبر خطوط الاتجاه أداة أساسية في تحليل سوق الأوراق المالية. فتساعد المستثمرين على اتخاذ قرارات مستنيرة (فاستر كابيتال، 2024).

اقرأ أيضاً ناقش كيف يُتيح مفهوم النهاية طريقة "للقسمة على 0"- واجبات unit 2 تفاضل وتكامل.

ما هي الدوال المشتقة؟

• يمكن استخدام المشتقة الأولى f'(t) لتحديد معدلات التغير في السعر. إذا كانت المشتقة إيجابية فإن السعر يرتفع. والعكس صحيح.
• المشتقة الثانية f′′(t) تساعد في فهم التسارع أو التباطؤ. وبالتالي تحديد إن كان الاتجاه الحالي مستدامًا أم لا. وبالتالي فإن أسواق المشتقات المالية قد نشأت لحماية الفرد من مخاطر أسواق المال. إلا أنه قد تحولت فيما بعد لأدوات تضاعف في حجم المخاطر التي من الممكن أن يتعرض لها النظام المالي (قندوز، 2022، ص22).

النسب المثلثية والدائرة المثلثية.

إذا كان هناك نمط دوري في سعر السهم (مثل ارتفاع وانخفاض منتظم). يمكنك استخدام النسب المثلثية لتحديد الفترات التي تصل فيها الأسعار إلى القمم أو القيعان.

تحليل الاتجاهات (Trend Analysis).

يمكنك رسم الخطوط البيانية لسعر السهم لتحديد الاتجاه العام (صعودي. هبوطي. أو عرضي). الاتجاه الصعودي يشير إلى فرص للشراء. بينما الاتجاه الهبوطي يشير إلى فرص للبيع أو تجنب الاستثمار (الاستثمار في التداول، 2024).

ما هي الأدوات التي يُمكن تطبيقها لنتمكن من كسب المال عن طريق شراء وبيع الأسهم؟

بفرض أن دالة ما. (f(t. تقوم بنمذجة سعر السهم في الوقت t. يمكن اقتراح نصائح تطبيقية مثل:
الشراء عند الانخفاض والبيع عند الارتفاع: استخدم هذه الأدوات لتحديد اللحظات التي يكون فيها سعر السهم أقل من قيمته المتوقعة.
إدارة المخاطر: لا تستثمر بناءً على أداة واحدة فقط؛ قم بتحليل شامل قبل اتخاذ قرارات الشراء أو البيع.
تطبيق التحليل الزمني: حاول فهم أنماط السوق على مدار أيام أو أسابيع لتحديد الوقت المثالي للاستثمار.

في الختام يمثل استخدام الأدوات الرياضية لتحليل أسعار الأسهم وسيلة فعالة لاتخاذ قرارات استثمارية مدروسة. من خلال فهم الاتجاهات. وتحديد نقاط التغير. واستكشاف الأنماط الدورية. يمكن للمستثمرين تعزيز فرص تحقيق الأرباح وتقليل المخاطر المرتبطة بتقلبات السوق.

المراجع.

1. الاستثمار في التداول. (2024). تحليل سوق الأسهم دليلك الشامل لفهم وتحليل أسواق الأسهم. تم الاسترجاع من الرابط https://investing-in-trading.com/stock-market-analysis/ .
2. فاستر كابيتال. (2024). الخطوط الاتجاه: تسخير قوة الخطوط الاتجاه في تحليل اتجاه الأسهم. فاستر كابيتال. تم الاسترجاع من الرابط https://2u.pw/Nx637vm2.
3. قندوز. عبد الكريم. (2022). كتيب المشتقات المالية. صندوق النقد العربي. العدد38. ملف pdf. تم الاسترجاع من الرابط https://2u.pw/bGLKXh.

--------------------------------------------------------------

الواجب الكتابي.

إن الحد الأدنى المطلق (أو ما يدعى بالقيمة الدنيا المطلقة) هي أصغر قيمة للدالة على كامل منطقة تعريفها (منطلقها أو Domain)

بينما الحد الأدنى محلياً (أو القيمة الدنيا المحلية) هي أصغر قيمة للدالة عندما تكون X بجوار C (البرقلي، 2010، ص320).

استخدم حساب التفاضل والتكامل لإيجاد الحد الأدنى المطلق (القيمة الدنيا المطلقة) من F(X) = X^2 – 6*X +2

لإيجاد الحد الأدنى المطلق للدالة F(x)=x2−6x+2 باستخدام حساب التفاضل والتكامل، نتبع الخطوات التالية:

1. 🔔 إيجاد المشتقة الأولى: نحسب المشتقة الأولى للدالة F(x):

F′(x)=d/dx(x2−6x+2)=2x−6

2. 🔔 إيجاد النقاط الحرجة: لحساب النقاط الحرجة، نحل المعادلة F′(x)=0 :

2x−6=0

x = 3 النقطة الحرجة الوحيدة هي x=3.

3. 🔔 التحقق من نوع النقطة الحرجة:

لحسم نوع النقطة الحرجة (حد أدنى أو حد أقصى)، نستخدم المشتقة الثانية:

F′′(x) = d/dx(2x−6)=2

بما أن F''(x) > 0 (ثابت موجب)، فإن النقطة x = 3 تمثل حدًا أدنى محليًا.

4. 🔔 حساب قيمة F(x) عند النقطة الحرجة: نعوض x = 3 في الدالة F(x) لنحسب القيمة:

F(3) =(3)2−6(3)+2=9−18+2=−7

5. 🔔 التحقق من الحد الأدنى المطلق: لأن الدالة F(x) هي دالة تربيعية ذات معامل رئيسي موجب x^2) معاملها موجب)، فإنها مفتوحة لأعلى، مما يعني أن الحد الأدنى المحلي عند x = 3 هو الحد الأدنى المطلق.

النتيجة: الحد الأدنى المطلق للدالة F(x)=x2−6x+2 هو: −7 عند x=3

ما هي القيم التي تحقق أن تكون الدالة F(X) = - sin X +cos X مقعرة نحو الأعلى في [0,2π]

لحساب القيم التي تكون فيها الدالة F(x) = - sin x + cos x مقعرة نحو الأعلى، نستخدم المشتقة الثانية للدالة. إليك الخطوات:

1. 🔑 المشتقة الأولى: نحسب المشتقة الأولى للدالة F(x):

F′(x) = d/dx(−sinx+cosx) = −cosx−sinx

2. 🔑  المشتقة الثانية: نحسب المشتقة الثانية: F′′(x) = d/dx(−cosx−sinx)=sinx−cosx

3. 🔑  شرط التحدب نحو الأعلى: للدالة أن تكون مقعرة نحو الأعلى، يجب أن تكون F′′(x)>0 :

sinx−cosx>0 أو: sinx > cosx

4. 🔑  حل المتباينة sinx>cosx في الفترة [0,2π]:

تحليل باستخدام الرسم البياني:

Sinx > cosx يحدث عندما تكون زاوية x أكبر من زاوية cosx = sinx ، أي عند x=π/4 وتستمر حتى تقطع sin x مع −cosx

الحل العددي: تحليل الفترة التي تحقق sinx > cosx:

1- المعادلة sinx = cosx:

• هذه المعادلة تتحقق عندما x=4π​+nπ حيث n∈Z.
• ضمن الفترة [0,2π]، القيم التي تحقق sinx = cosx هي: X = π/4و X = 5π/4

2- الإشارة في الفترة [0,2π]:

• بين x=0 وx=π/4 : cosx>sinx القيمة العظمى لـ cosx عند x=0).).
• بين x=π/4x​ و) sin x > cos : x=5π/4 القيمة العظمى لـ sinx عند x=π2 ).
• بين x=5π/4 و x=2π: cosx>sinx (القيمة العظمى لـ cosx عند x =2π.).

الفترة المطلوبة: الدالة تكون مقعرة نحو الأعلى عندما sinx>cosx، أي: x∈(π/4,5π/4).

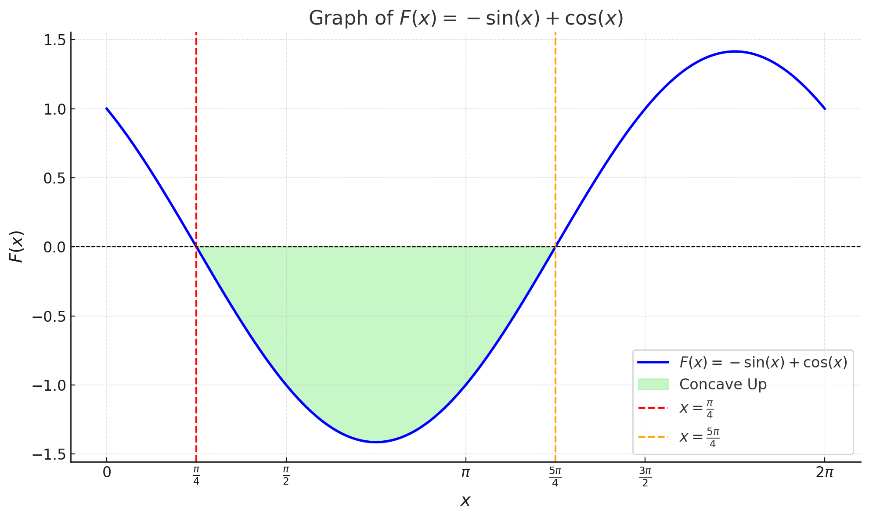
الرسم البياني:

يمثل sinx و cosx دوال دورية تتقاطع عند x=π/4 و x=5π/4

في الفترة (π/4,5π/4 ​)، تكون sinx > cosx، وبالتالي F′′(x) > 0، مما يعني أن F(x) مقعرة نحو الأعلى.

 

هذا هو الرسم البياني للدالة F(x) = -sin(x) + cos(x).

المنطقة المظللة بالأخضر تمثل الفترة (π/4,5π/4)، حيث تكون الدالة مقعرة نحو الأعلى (F′′(x)>0).

أوجد النهاية lim x→4 ((x^2-16)/(x-4))

لحساب النهاية limx→4 (x2−16/x−4) ، نلاحظ أن تعويض x = 4 يؤدي إلى الشكل غير المحدد 0/0 لذا نحتاج إلى تبسيط التعبير.

الخطوات: 

🔆- تبسيط البسط: x2−16 هو فرق بين مربعين: x2−16 = (x−4)(x+4)

إذن التعبير يصبح: {x2−16/x−4} ={ (x - 4)(x + 4)/(x – 4)}

🔆- إلغاء العامل المشترك: طالما x≠4 ، يمكننا إلغاء x - 4:

{(x - 4)(x + 4)}/{x - 4} = x + 4

🔆- حساب النهاية: الآن نعوض x = 4 في التعبير المبسط x+4:

limx→4(x+4) =4+4=8

المراجع.

1. البرقلي، ناديا. (2010). أساسيات التفاضل والتكامل وتطبيقاتهما. الفصل الثالث. ط1. مكتبة المنهل. ملف pdf. تم الاسترجاع من الرابط https://2u.pw/Vs3s7Hpf.  

----------------------------------------------------------------------

مجلة التعلم.

ما هو حل مشكلة عدم فهم الرياضيات؟

ان تعلم الرياضيات يتضمن تعلم القراءة والكتابة للمفاهيم الرياضية والاستماع لنظرياتها وفهم قواعد التعبير بها، ومن خلال الكتابة الرياضية يمكن التعبير عن فكرة بلغة واضحة وتنظيم متسق لإقناع المستمع (عبد الله، 2019، ص2).

تتمثل الكتابة الرياضية في إمكانية استخدام لغة الرياضيات المكتوبة، وتقديم وصف لفظي لكيفية وطرق حل مسألة لفظية، وتقديم وصف رياضي مكتوب لنموذج رياضي محدد، فمهارات الكتابة تساعد على تثبيت الأفكار، وتدعيم مهارات التواصل الرياضي (الأسمري وآخرون، 2023، ص143).

الكتابة الرياضية تتميز بلغة خاصة ورموز محددة، مما يجعلها أكثر صعوبة في الفهم من النصوص العادية. أسباب هذه الصعوبة تشمل:

• الكثافة المعلوماتية: تحوي المعادلة الرياضية كمية كبيرة من المعلومات في مساحة صغيرة.
• الرمزية: تستخدم الرموز الرياضية لتمثيل مفاهيم مجردة، مما يتطلب فهماً عميقاً لهذه المفاهيم.
• التسلسل المنطقي: تتطلب فهم المعادلة الرياضية تتبع تسلسل منطقي محدد.

الأجزاء النص الأكثر صعوبة في القراءة

إن الأجزاء النص الأكثر صعوبة في القراءة هي كالتالي:

1. التعريفات والمصطلحات الرياضية: مثل "هامش المساهمة" و"نقطة التعادل"، قد تكون صعبة إذا لم يتم شرحها بتفصيل كافٍ أو من دون أمثلة ملموسة.
2. الجملة التي تربط هامش المساهمة بالتكاليف الثابتة ("هامش المساهمة هو الفرق بين سعر البيع والتكلفة المتغيرة...") قد تبدو معقدة إذا كنت غير معتاد على المفهوم.
3. الصيغ والمعادلات والتعبيرات الرياضية مثل هامش المساهمة لكل وحدة=سعر البيع−التكلفة المتغير، تبدو مباشرة، ولكن قد يكون فهم تطبيقها العملي أكثر صعوبة.
4. حساب نسبة هامش المساهمة وإدراج القيم داخل الصيغ كان قد يتطلب إعادة قراءة للتأكد من أن الأرقام والتفسير مترابطان بشكل صحيح.
5. التحليل والتفسير للنتائج الرياضية بعد العمليات الحسابية (مثل سبب اختيار المنتج أ أو ب بناءً على النتائج) هو جزء يحتاج إلى استيعاب السياق والبيانات المقدمة.
6. التوزيع غير الصحيح لساعات العمل بناءً على نسبة هامش المساهمة بدلاً من هامش المساهمة لكل ساعة قد يكون مربكًا.

أجزاء النص الأكثر صعوبة في القراءة

وتختلف أجزاء النص الأكثر صعوبة في القراءة حسب عدة عوامل، منها:

1. المستوى اللغوي: وجود مصطلحات علمية أو تقنية غير مألوفة، أو استخدام جمل طويلة ومعقدة.
2. المحتوى المعرفي: تتطلب بعض النصوص خلفية معرفية سابقة في مجال معين، مما يجعل فهمها صعباً لمن لا يمتلك هذه الخلفية.
3. التركيب النحوي: وجود جمل طويلة أو جمل تحتوي على شروط أو استثناءات قد تزيد من صعوبة الفهم.
4. الرموز والتعبيرات الرياضية: في النصوص الرياضية، تعتبر الرموز والمعادلات من أكثر الأجزاء التي تستغرق وقتاً لفهمها.

عدد المرات التي تمت فيها قراءة المقطع قبل تحقيق الفهم:

بعض التعريفات قد تحتاج إلى قراءة واحدة أو اثنتين لفهم الفكرة الأساسية، ولكن قد تتطلب بعض المصطلحات المزيد إذا كانت جديدة.
الصيغ والمعادلات: غالبًا يتم قراءة هذه الأجزاء مرتين أو ثلاث مرات للتأكد من فهم الأرقام وتطبيقها.

بعض العوامل التي تؤثر على هذا العدد هي:

• تعقيد النص: النصوص المعقدة تحتاج إلى قراءات متكررة أكثر من النصوص البسيطة.
• التركيز والانتباه: القراءة المتأنية والتركيز على كل كلمة وجملة يساعدان على الفهم بشكل أسرع.
• الخلفية المعرفية: القارئ الذي يمتلك خلفية معرفية في الموضوع يستطيع فهم النص بشكل أسرع.
• أسلوب القراءة: هناك العديد من أساليب القراءة التي يمكن استخدامها لتحسين الفهم، مثل القراءة بصوت عالٍ، أو تسليط الضوء على الكلمات الرئيسية، أو أخذ الملاحظات.

استراتيجيات تحسين الفهم لتلك المصطلحات والمفاهيم.

يمكن ادراج بعض الاقتراحات لتحسين الفهم لتلك المصطلحات والمفاهيم مثل:

1. إضافة أمثلة تطبيقية لتقوم بشرح مفصل لكل مفهوم جديد.
2. تقسيم النصوص الرياضية وتنظيم المعلومات بخطوات واضحة وبسيطة لتسهيل الفهم التدريجي.
3. التأكيد على أهمية التحقق فإعادة قراءة النصوص الرياضية هو جزء طبيعي من عملية الفهم.

المراجع.

1. الأسمري، نورة عوضه ومحمد، رشا هاشم وخليل، إبراهيم الحسين. (2024). التحديات التي تواجه معلمي الرياضيات عند تنمية مهارات الكتابة الرياضية لدى طلابهم. العدد171. المجلد 45. رسالة الخليج العربي.
2. عبد الله، مدركة صالح. (2019). التواصل الرياضي وفق معايير NCTM. المحاضرة العاشرة.