أنماط التعلم - ما هي أنماط التعلم لدى المتعلمين

 

ما هي قاعدة السلسلة؟

قاعدة السلسلة هي إحدى أهم القواعد المستخدمة على نطاق واسع في حسابات التفاضل والتكامل. والتي تتيح لنا العثور على المشتق لوظيفة مركبة. والمكونة من وظيفتين او أكثر. 

بمعنى آخر هي أداة أساسية لإيجاد مشتق من مجموعة متعددة من الوظائف. كما تتيح لنا هذه القاعدة أخذ مشتق وظيفة في داخل وظيفة أخرى (فاستر كابيتال، 2024).

لماذا يجب عليك استخدام قاعدة السلسلة؟

استخدام قاعدة السلسلة في التفاضل يصبح مفضلاً ومفيداً عند التعامل مع الدوال ذات الدرجات العالية أو الدوال المركبة للأسباب التالية:

1- تُبسِّط الحسابات:

• عندما تكون لديك دالة مركبة (مثل (3x^2 + 2)^5 أو( sin(x^3). يمكن أن يكون التفاضل المباشر صعباً وغير عملي.
• قاعدة السلسلة تُقسِّم المشكلة إلى أجزاء أبسط: تُشتق الدالة الخارجية أولاً ثم تُضرب في مشتقة الدالة الداخلية.

2- تقلل الأخطاء:

• التفاضل المباشر لدالة مركبة يزيد احتمالية الأخطاء في العمليات الحسابية.
• باستخدام قاعدة السلسلة. هناك خطوات منهجية وواضحة لتفاضل كل جزء من الدالة.

3- فعّالة للدوال المتكررة أو المركبة:

• عند العمل مع دوال مركبة مكررة (مثل ((f(g(x)))^n). تكون قاعدة السلسلة هي الأنسب لتفادي التفكيك المعقد للدالة.

4- تسهل معالجة الدوال الضمنية:

• في الحالات التي تكون فيها الدالة معرّفة ضمنياً (مثل y في (y^2 + x^2 = 1). تُستخدم قاعدة السلسلة بشكل مباشر للتعامل مع العلاقات بين المتغيرات.

مثال عملي: لتوضيح السبب. دعنا نأخذ الدالة: h(x) = (3x^2 + 2)^5

• بدون قاعدة السلسلة: تحتاج إلى توسيع القوس ورفع كل حد للقوة الخامسة. ثم تفاضل الناتج. وبالتالي هذا الأمر قد يكون معقداً وطويلاً.

باستخدام قاعدة السلسلة:

• نعتبر u = 3x^2 + 2، ومن ثم: h(x) = u^5
• اشتقاق الدالة الخارجية : d/dx [u^5] = 5u^4 .
• ثم ضربها بمشتقة الدالة الداخلية: u = 3x^2 + 2 .

d/dx [h(x)] = 5(3x^2 + 2)^4 * 6x .

الناتج النهائي d/dx [h(x)] = 30x(3x^2 + 2)^4 .

النتيجة: قاعدة السلسلة توفر وقتاً وجهداً كبيرين عند التعامل مع الدوال ذات الدرجات العالية أو المركبة.


في الختام 👈 بالنسبة لسبب استخدام قاعدة السلسلة بالنسبة للدوال ذات الدرجات العليا:

ذلك بشكل أساسي من أجل تحقيق الدقة فى الحسابات. و توفير الوقت و الجهد.

حيث أنه فى اشتقاق الدوال ذات الدرجات العليا. يُمكن: 

1. فك الأقواس بإستخدام نظرية ذات الحدين Binomial Theorem. والتي يتم استخدامها بشكل أساسي. للحصول على المفكوك لحدين (مجموعين أو مطروحين) مرفوعين لأس عدد صحيح موجب كبير يكون أكبر من 3؛ كمثلا 4 أو 10 أو أكثر. ومن ثم يتم الحصول على مقدار كثير الحدود.
2. يتم اشتقاق كل حد على حدى و لكن ستكون حدود عديدة. وسيتطلَّب ذلك حسابات جبرية كثيرة.

اقرأ أيضاً مفهوم السرعة - كيف يُمكن استخدام "السرعة" في الحياة الواقعية - واجبات Unit 1 تفاضل وتكامل

اقرأ أيضاً كيف يُمكن استخدام التكامل المحدود لتحديد الربح خلال فترة معينة؟- واجبات Unit 8 تفاضل وتكامل.

ونتيجة هذه الحسابات؛ قد يستغرق ذلك وقتا أطول. و كذلك قد يكون هناك خطأ فى الحسابات لوجود حدود كثيرة. ولذلك يتم استخدام قاعدة السلسة مباشرة فى اشتقاق الدوال ذات الدرجات العليا. فهى توفر الوقت والجهد والحسابات الجبرية الكثيرة؛ مما يضمن الحصول على نتائج أكثر دقة.
--------------------------------------------------------

الواجب الكتابي.

1 – ما هو مشتق f(x) = cos (x^4) ؟

نستخدم قاعدة السلسلة لأننا نتعامل مع دالة مركبة:

مشتقة cos(u) بالنسبة إلى u هي: −sin (u)

نشتق الدالة الداخلية    u = x^4 لنحصل على 4x^3.

المشتقة:    

 f'(x) =   − sin (u) * 4x^3

f'(x) = - sin(x^4) *4x^3 = - 4x^3 sin(x^4)

2- ما هو مشتق g(x) = (cos x)^4 ؟

أيضاً نستخدم قاعدة السلسلة لأن الدالة مرفوعة لقوة.

نعتبر u = cos(x)، ثم g(x) = u^4

نشتق u^4  بالنسبة إلى (u) :   4u^3

نضرب في مشتقة الدالة الداخلية u = cos(x): مشتقتها هي −sin (x)

المشتقة: g'(x) = 4(cos(x))^3 * (-sin(x)) = -4(cos(x))^3 *sin(x)

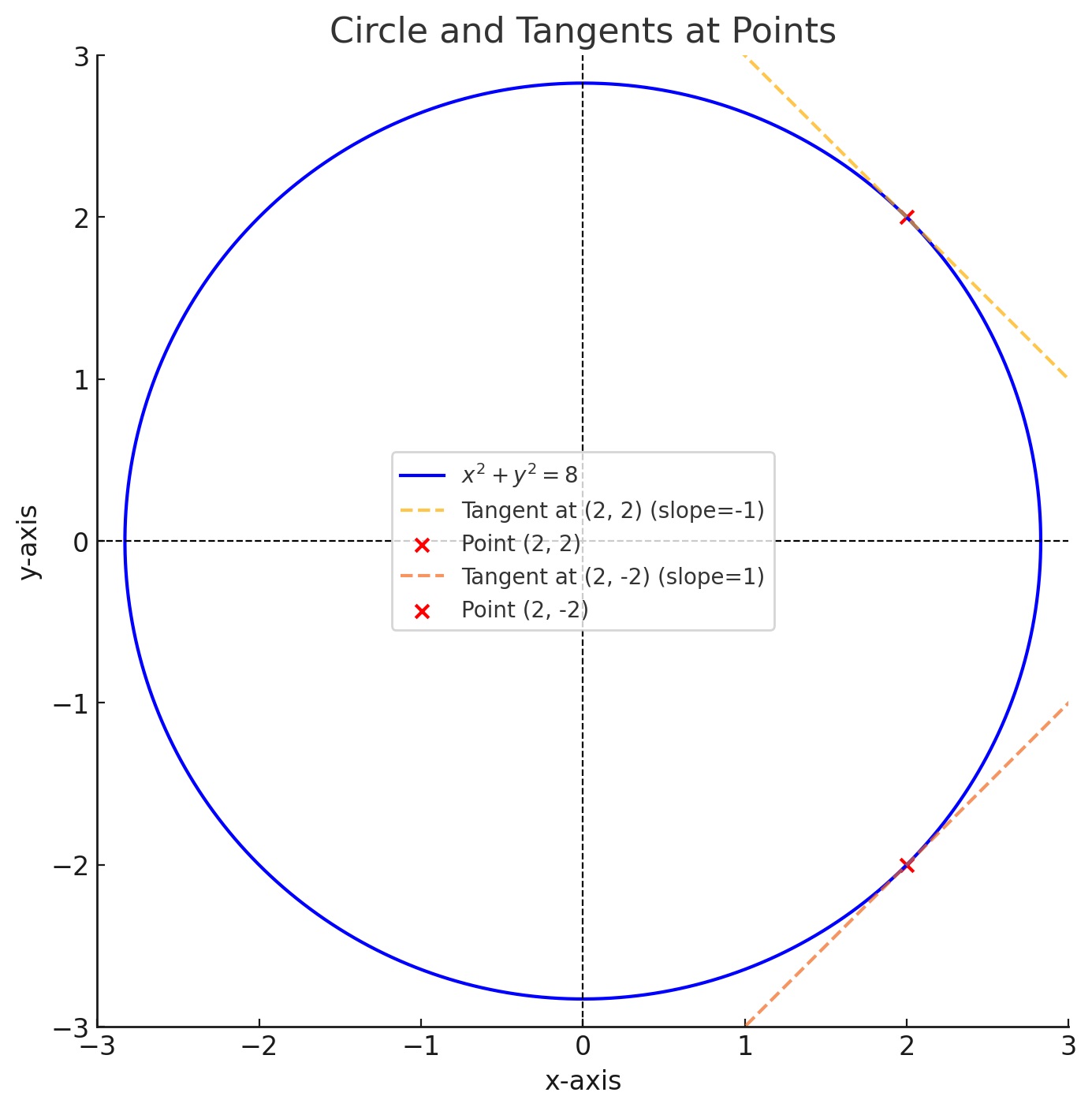
3- استخدم التفاضل الضمني للعثور على Y من x^2+ y^2 في (2,2) وفي (2,-2) 

(قد يكون من المفيد إلقاء نظرة على الرسم البياني)

الخطوات:

نشتق الطرفين بالنسبة إلى x مع اعتبار y دالة تعتمد على ) x أي نستخدم قاعدة السلسلة لـ (y^2):

d /dx [x^2 + y^2] = d/dx [8]

مشتقة x^2 هي 2x ومشتقة y^2 هي 2y⋅dy/dx (قاعدة السلسلة)، ومشتقة العدد 8 هي صفر:

2x + 2y * (dy/dx) = 0

نبسط ونحل بالنسبة إلى dy/dx :

2y * (dy/dx) = −2x

dy/dx = − x/y

إيجاد ميل المماس عند النقاط:

النقطة (2, 2):  dy/dx =  −2/2 =  −1

النقطة (2, -2) :  dy/dx = −2/−2 =  1

في الختام  الرسم البياني يمثل دائرة مركزها عند الأصل ونصف قطرها 8 √ عند النقطة (2, 2)، يكون الميل سالباً (-1) لأن المماس يميل للأسفل. أما عند (2, -2)يكون الميل موجباً (1) لأن المماس يميل للأعلى.

----------------------------------------------------------

مجلة التعلم.

ما هي قاعدة السلسلة للتفاضل الضمني؟

قاعدة السلسلة والتفاضل الضمني هما من المواضيع المتقدمة في حساب التفاضل والتكامل، ويمكن أن تكون صعبة في البداية بسبب تعقيد العمليات الرياضية.

أولاً - قاعدة السلسلة.

هي تقنية أساسية في التفاضل حيث تتعلق بتفاضل دالة مركبة. بمعنى آخر هي أداة أساسية لإيجاد مشتق من مجموعة متعددة من الوظائف بقصد تبسيط الحسابات وتقليل الأخطاء. كما تتيح لنا هذه القاعدة أخذ مشتق وظيفة في داخل وظيفة أخرى (فاستر كابيتال، 2024).

تُعد قاعدة السلسلة أداةً أساسيةً في حساب التفاضل. خاصةً عند التعامل مع الدوال المركبة ذات الدرجات العليا. لا تقتصر أهميتها على تبسيط عملية الاشتقاق فحسب. بل تمتد إلى تعميق الفهم للعلاقات بين المتغيرات.، وتحليل السلوك الرياضي والفيزيائي للأنظمة المعقدة.

حيث إذا كان لدينا دالة على الشكل: y=f(g(x)) فإن مشتقة y بالنسبة لـ x تُعطى بـ: dy/dx=f′(g(x))⋅g′(x)

مثال على قاعدة السلسلة.

إذا كانت y = (3x^2 + 1)^5:

• نعتبر g(x)= 3x^2 + 1 و f(u) = u^5، حيث u = g(x).
• المشتقة f'(u) = 5u^4 و g′(x)=6x
• باستخدام قاعدة السلسلة:

dy/dx=f′(g(x))⋅g′(x)= 5(3x^2 + 1)^4 *6x = 30x(3x^2 + 1)^4

إيجاد مشتقة الدالة المركبة يتطلب في البداية فهم كل جزء من الأجزاء المعقدة، ما قد يصعب الفهم في البداية.

ما هي التطبيقات العملية لقاعدة السلسلة؟

أبرز تطبيقات قاعدة السلسلة تشمل:

1. الدوال متعددة الأبعاد: تُستخدم لحساب المشتقات الجزئية لكل متغير مستقل، مما يُسهل دراسة التغيرات والسلوك في هذه الدوال.
2. التطبيقات العلمية: في الفيزياء، تُطبق لتحليل سرعة التغير والتسارع والقوى في الحركة والديناميكا.
3. المجالات الهندسية: تُساهم في تحليل الأنظمة المعقدة وحساب الميزانيات، مثل نمذجة الظواهر الديناميكية.

كيفية تطبيق قاعدة السلسلة.

فيتم تطبيق قاعدة السلسلة chain rule ، حيث يتم تطبيقها على خطوتين كالتالي:

أولا: يتم ترك الدالة الداخلية h(x) كما هي، ومن ثم يتم أخذ الاشتقاق للدالة الخارجية g(x)؛ فنحصل على g'

ثانيا: يتم ضرب الناتج ((g'(h(x في اشتقاق الدالة الداخلية h'(x).

ومثال على تطبيق قاعدة السلسلة؛ ايجاد الاشتقاق للدالة f(x)

وأضيف أنه للتأكد من حلك باستخدام قاعدة السلسلة؛ يمكنك استخدام حاسبة symbolab

ثانياً - التفاضل الضمني.

يُستخدم عندما نحتاج لتفاضل دوال تحتوي على متغيرات بشكل غير مباشر (مثل y في معادلة تحتوي على x و y) عند تطبيق التفاضل الضمني، نستخدم القاعدة العامة للتفاضل.

 مع اعتبار أن y هو دالة في x وبالتالي مشتقة y ستكون dy/dx .

بمعنى آخر يُستخدم التفاضل الضمني عندما تكون الدالة غير مُعطاة بشكل صريح y = f(x) ولكنها مُعطاة ضمن علاقة بين x و y، مثل F(x, y) = 0.

لتفاضل مثل هذه العلاقات، نعتبر y دالة ضمنية في x ونطبق قاعدة السلسلة.

d/dx[F(x,y)] = ∂F/∂x + ∂F/∂y⋅dy/dx = 0

ثم نحل لإيجاد dy/dx.

مثال على التفاضل الضمني.

إذا كانت العلاقة: x^2 + y^2 = 25

1. نفرض أن y = y(x)، ونفاضل الطرفين بالنسبة إلى x:

d/dx[x^2] + d/dx[y^2] = d/dx [25]

2. المشتقة: 2x+2y⋅dy/dx=0

3. حل لإيجاد dy/dx : dy/dx=−x/y

الأجزاء من النص التي قد تكون أكثر صعوبة في قراءتها:

1. قاعدة السلسلة: قد تكون فكرة التعامل مع الدوال المركبة (مثل f(g(x))) والتعرف على كيفية تطبيق قاعدة السلسلة غير مألوفة للبعض، خصوصًا عند التفريق بين f'(g(x))و g'(x).
2. التفاضل الضمني: إن الخطوة التي تتطلب افتراض أن y دالة ضمنية تعتمد على x قد تبدو غير واضحة.
3. الأمثلة: إذا كان القارئ غير ملم بكيفية العمل مع المشتقات الأساسية.، مثل مشتقة x^n أو مفهوم قاعدة السلسلة، فربما يجد بعض الصعوبة في تتبع الأمثلة، خاصة عند وجود خطوات متعددة.

بالنسبة للصعوبة في القراءة والفهم، قد يكون من الصعب في البداية فهم كيف تنطبق القواعد في سياقات متعددة، وأحيانًا يحتاج النص إلى عدة قراءات قبل أن تتضح الفكرة. ستحتاج إلى التمرين على تطبيق القواعد في مسائل مختلفة لفهمها بشكل أعمق.


لتبسيط النص، يمكن تقسيم الخطوات إلى أجزاء أصغر وشرح كل جزء بمزيد من التفصيل مع توضيح الأسباب وراء كل خطوة.

المراجع.

1. فاستر كابيتال. (2024). قاعدة السلسلة: تطبيقه على مشتق التدفق. فاستر كابيتال. تم الاسترجاع من الرابط https://2u.pw/4vh1B3K.